Model of the system
3D linear inverted pendulum is used as an approximate model of a humanoid robot.
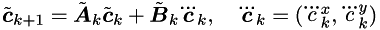
![$ \mbm{A} = \left[\hspace{-0.1cm} \begin{array}{cccccc} 1 & T_k & T_k^{2}/2 & 0 & 0 & 0 \vspace{0.05cm}\\ 0 & 1 & T_k & 0 & 0 & 0 \vspace{0.05cm}\\ 0 & 0 & 1 & 0 & 0 & 0 \vspace{0.05cm}\\ 0 & 0 & 0 & 1 & T_k & T_k^{2}/2 \vspace{0.05cm}\\ 0 & 0 & 0 & 0 & 1 & T_k \vspace{0.05cm}\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \hspace{-0.1cm}\right], \quad \mbm{B}_k = \left[\hspace{-0.1cm} \begin{array}{cc} T_k^{3}/6 & 0 \vspace{0.05cm} \\ T_k^{2}/2 & 0 \vspace{0.05cm} \\ T_k & 0\\ 0 & T_k^{3}/6 \vspace{0.05cm} \\ 0 & T_k^{2}/2 \vspace{0.05cm} \\ 0 & T_k \end{array} \right] $](form_1.png)
Where 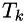 is a time sampling period in the preview window.
is a time sampling period in the preview window.
Originally the state vector is defined as 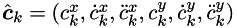 where
where 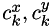 are coordintes of the center of mass.
are coordintes of the center of mass.
Variable substitutions
The first substitution
After the first variable substitution we get 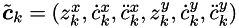 where
where 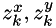 are coordintes of the ZMP.
are coordintes of the ZMP.
The state and control input matrices are changed accordingly:
![$ \tilde{\mbm{A}} = \left[ \begin{array}{cccccc} 1 & T_k & T_k^{2}/2-\Delta h_k & 0 & 0 & 0 \vspace{0.05cm}\\ 0 & 1 & T_k & 0 & 0 & 0 \vspace{0.05cm}\\ 0 & 0 & 1 & 0 & 0 & 0 \vspace{0.05cm}\\ 0 & 0 & 0 & 1 & T_k & T_k^{2}/2-\Delta h_k \vspace{0.05cm}\\ 0 & 0 & 0 & 0 & 1 & T_k \vspace{0.05cm}\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right], \quad \tilde{\mbm{B}} = \left[ \begin{array}{cc} T^{3}/6-hT & 0 \\ T^{2}/2 & 0\\ T & 0\\ 0 & T^{3}/6-hT \\ 0 & T^{2}/2\\ 0 & T \end{array} \right] $](form_7.png)
Here 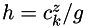 , i.e. the height of center of mass divided by the norm of gravitational acceleration;
, i.e. the height of center of mass divided by the norm of gravitational acceleration;
The second substitution
The last substitution rotates the state vector using matrix
![$ \bar{\mbm{R}}_k = \left[ \begin{array}{cccccc} \cos\theta_k & 0 & 0 & -\sin\theta_k & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \sin\theta_k & 0 & 0 & \cos\theta_k & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right]. $](form_9.png)
where 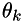 is an angle with respect to the world frame.
is an angle with respect to the world frame.
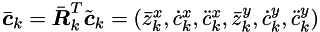
Objective function
Output matrices for position and velocity:
![$ \mbm{C}_p = \left[ \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array}\right], \quad \mbm{C}_v = \left[ \begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \end{array}\right], $](form_12.png)
![$ \bar{f}(\bar{\mbm{v}}) = \left[\hspace{-0.1cm}\begin{array}{c} \bar{\mbm{v}}_c \\ \mbm{v}_u \end{array}\hspace{-0.1cm}\right]^T \left[\hspace{-0.1cm}\begin{array}{cc} \tilde{\mbm{H}}_c & \mbm{0} \\ \mbm{0} & \mbm{H}_u \end{array}\hspace{-0.1cm}\hspace{-0.1cm}\right] \left[\hspace{-0.1cm}\begin{array}{c} \bar{\mbm{v}}_c \\ \mbm{v}_u \end{array}\hspace{-0.1cm}\right] + \left[\hspace{-0.1cm}\begin{array}{c} \bar{\mbm{v}}_c \\ \mbm{v}_u \end{array}\hspace{-0.1cm}\right]^T \left[\hspace{-0.1cm}\begin{array}{c} \bar{\mbm{g}}_c \\ \mbm{0} \end{array}\hspace{-0.1cm}\right] $](form_13.png)
where
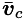 is a column vector containing state vectors and
is a column vector containing state vectors and 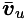 is a column vector containing control inputs.
is a column vector containing control inputs.
or
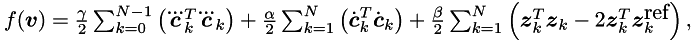
![$\\ \mbm{H}_u = \left[ \begin{array}{ccc} \mbm{P} & \dots & \mbm{0} \\ \vdots & \ddots & \vdots \\ \mbm{0} & \dots & \mbm{P} \\ \end{array} \right],\quad \mbm{P} = \left[ \begin{array}{cc} \frac{\gamma}{2} & 0 \\ 0 & \frac{\gamma}{2} \\ \end{array} \right];\\ \tilde{\mbm{H}}_c = \left[ \begin{array}{ccc} \tilde{\mbm{Q}} & \dots & \mbm{0} \\ \vdots & \ddots & \vdots \\ \mbm{0} & \dots & \tilde{\mbm{Q}} \\ \end{array} \right], \quad \tilde{\mbm{Q}} = \left[ \begin{array}{cccccc} \frac{\beta}{2} & 0 & 0 & 0 & 0 & 0\\ 0 & \frac{\alpha}{2} & 0 & 0 & 0 & 0\\ 0 & 0 & r & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{\beta}{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{\alpha}{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & r \\ \end{array} \right] $](form_19.png)
Here 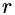 is a regularization factor, which makes the matrix nonsingular.
is a regularization factor, which makes the matrix nonsingular.
Equality constraints
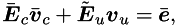
where 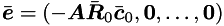 ,
,
![$ \bar{\mbm{E}}_c = \left[ \begin{array}{cccccc} -\bar{\mbm{R}}_1 & \mbm{0} & \mbm{0} & \dots & \mbm{0} & \mbm{0} \\ \mbm{A}\bar{\mbm{R}}_1 & -\bar{\mbm{R}}_2 & \mbm{0} & \dots & \mbm{0} & \mbm{0} \\ \mbm{0} & \mbm{A}\bar{\mbm{R}}_2 & -\bar{\mbm{R}}_3 & \dots & \mbm{0} & \mbm{0} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \mbm{0} & \mbm{0} & \mbm{0} & \dots & \mbm{A}\bar{\mbm{R}}_{N-1} & -\bar{\mbm{R}}_N \\ \end{array} \right], \quad \tilde{\mbm{E}}_u = \left[ \begin{array}{cccc} \tilde{\mbm{B}} & \dots & \mbm{0} \\ \vdots & \ddots & \vdots \\ \mbm{0} & \dots & \tilde{\mbm{B}} \\ \end{array} \right]. $](form_23.png)
See page 'Derivation of the matrix of equality constraints' for example.
Inequality constraints
![$ \left[ \begin{array}{cccccc} -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{array} \right]\bar{\mbm{c}}_k + \mbm{d}_{k} \geq \mbm{0}, $](form_24.png)
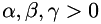 are gains.
are gains.![$ \frac{\beta}{2}\mbm{z}_k^T\mbm{z}_k - \beta\mbm{z}_k^T\mbm{z}^{\mbox{ref}}_k = \bar{\mbm{c}}_k^T\frac{\beta}{2}\mbm{C}_p^T\mbm{C}_p\bar{\mbm{c}}_k - \bar{\mbm{c}}_k^T\underbrace{\bar{\mbm{R}}^T_k\beta\mbm{C}_p^T\mbm{z}^{\mbox{ref}}_k}_{\bar{\mbm{q}}_k}, \\ \bar{\mbm{v}}_c = \left[\begin{array}{c} \bar{\mbm{c}}_1 \\ \vdots \\ \bar{\mbm{c}}_N \end{array} \right], \quad \bar{\mbm{g}}_c = \left[\begin{array}{c} -\bar{\mbm{q}}_1 \\ \vdots \\ -\bar{\mbm{q}}_N \end{array} \right], \quad \bar{\mbm{v}} = \left[\begin{array}{c} \bar{\mbm{v}}_c \\ \mbm{v}_u \end{array} \right] $](form_18.png)
 1.8.0
1.8.0