A sparse MPC solver for walking motion generation (old version).: Derivations for the SMPC scheme

Inequality constraints:

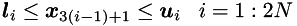
$\mbm{l}_i \le \mbm{x}_{3(i-1) + 1} \le \mbm{u}_i \;\;\; i = 1:2N$

Objective function + logarithmic barrier:

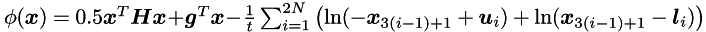
$\phi(\mbm{x}) = 0.5 \mbm{x}^T \mbm{H} \mbm{x} + \mbm{g}^T \mbm{x} -\frac{1}{t} \sum^{2N}_{i=1} \left( \ln (-\mbm{x}_{3(i-1) + 1} + \mbm{u}_i) + \ln (\mbm{x}_{3(i-1) + 1} - \mbm{l}_i) \right)$

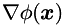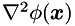$\nabla\phi(\mbm{x})$ and $\nabla^2\phi(\mbm{x})$ are defined as follows:

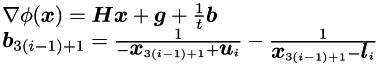
$\\ \nabla\phi(\mbm{x}) = \mbm{H}\mbm{x} + \mbm{g} + \frac{1}{t} \mbm{b}\\ \mbm{b}_{3(i-1) + 1} = \frac{1}{-\mbm{x}_{3(i-1) + 1} + \mbm{u}_i} - \frac{1}{\mbm{x}_{3(i-1) + 1} - \mbm{l}_i}$

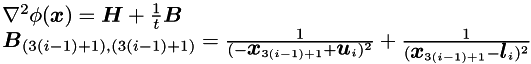
$\\ \nabla^2\phi(\mbm{x}) = \mbm{H} + \frac{1}{t} \mbm{B}\\ \mbm{B}_{(3(i-1) + 1),(3(i-1) + 1)} = \frac{1}{(-\mbm{x}_{3(i-1) + 1} + \mbm{u}_i)^2} + \frac{1}{(\mbm{x}_{3(i-1) + 1} - \mbm{l}_i)^2}$

A diagonal 6x6 matrix, which lies on the main diagonal of 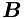$\mbm{B}$ and corresponds to state k, is denoted 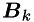$\mbm{B}_k$ . Each such matrix has only two non-zero elements: (1,1) and (4,4).

Schur complement (IP method)

The Schur complement for the new objective function is defined in a similar way as for the original objective (see 'Schur complement'). The part of the hessian corresponding to the vector of states is defined differently though.

$\\ \bar{\mbm{E}}_c\tilde{\mbm{H}}_c^{-1}\bar{\mbm{E}}_c^T = \\ = \left[ \begin{array}{ccccc} \mbm{M}_{11} & -\mbm{M}_{11}\mbm{A}^T & \mbm{0} & \mbm{0} & \mbm{0} \\ -\mbm{A}\mbm{M}_{11} & \mbm{A}\mbm{M}_{11}\mbm{A}^T + \mbm{M}_{22} & -\mbm{M}_{22}\mbm{A}^T & \mbm{0} & \mbm{0} \\ \mbm{0} & -\mbm{A}\mbm{M}_{22} & \mbm{A}\mbm{M}_{22}\mbm{A}^T + \mbm{M}_{33} & -\mbm{M}_{33}\mbm{A}^T & \mbm{0} \\ \mbm{0} & \mbm{0} & -\mbm{A}\mbm{M}_{33} & \mbm{A}\mbm{M}_{33}\mbm{A}^T + \mbm{M}_{44} & -\mbm{M}_{44}\mbm{A}^T \\ \mbm{0} & \mbm{0} & \mbm{0} & -\mbm{A}\mbm{M}_{44} & \mbm{A}\mbm{M}_{44}\mbm{A}^T + \mbm{M}_{55} \end{array} \right]$

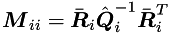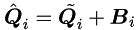where $\mbm{M}_{ii} = \bar{\mbm{R}}_i\hat{\mbm{Q}}^{-1}_i\bar{\mbm{R}}_i^T$ and $\hat{\mbm{Q}}_i = \tilde{\mbm{Q}_i} + \mbm{B}_i$ .